Unsupervised Thoughts A blog on machine learning

Accelerating LLM Code Generation Through Mask Store Streamlining

Structured text generation techniques enforcing context-free grammar (CFG) constraints (Willard & Louf, 2023; Gerganov & et. al., 2024; Lundberg & Ribeiro, 2023; Geng et al., 2024; Beurer-Kellner et al., 2024; Ugare et al., 2024; Dong et al., 2024) are particularly useful to generate syntatically correct computer code in the context of LLM-based coding tools. These techniques guarantee full compliance but introduce computational overhead at inference time.

Minimizing inference overhead is essential for a productive developer experience, especially when suggesting generated code in real time. This is challenging because the CFG of programming languages are complex and CFG constraints are harder to impose than regex constraints.

In this blog post, I propose to accelerate some CFG-constrained decoding techniques. More precisely, I will:

The code to reproduce the experimental results and the proofs of the algorithms are provided in a Python notebook and a technical appendix.

CFG-Constrained LLM Decoding

This blog post focuses on CFG-constrained decoding techniques (Beurer-Kellner et al., 2024; Willard & Louf, 2023) that leverage:

In this section, I will illustrate how these two components can be used, using the Python grammar as an example. I will only give a high-level overview, without covering secondary technical details (ignored terminals, terminal priorities, indentations). I invite you to read the papers referenced above, as well as the associated Python notebook, for a more comprehensive introduction.

The Python grammar as specified in the lark package includes:

Producing a string that can be converted into a sequence of terminals

When leveraging an incremental parser, a first step to ensure syntactically correct Python code generation is constructing a non-deterministic finite automaton (NFA) that recognizes strings convertible into terminal sequences. For this, we can simply connect the deterministic finite automata (DFA) corresponding to the regular expression of each terminal with \(\epsilon\) transitions and two additional nodes, as shown on Figure 1 for a few terminals.

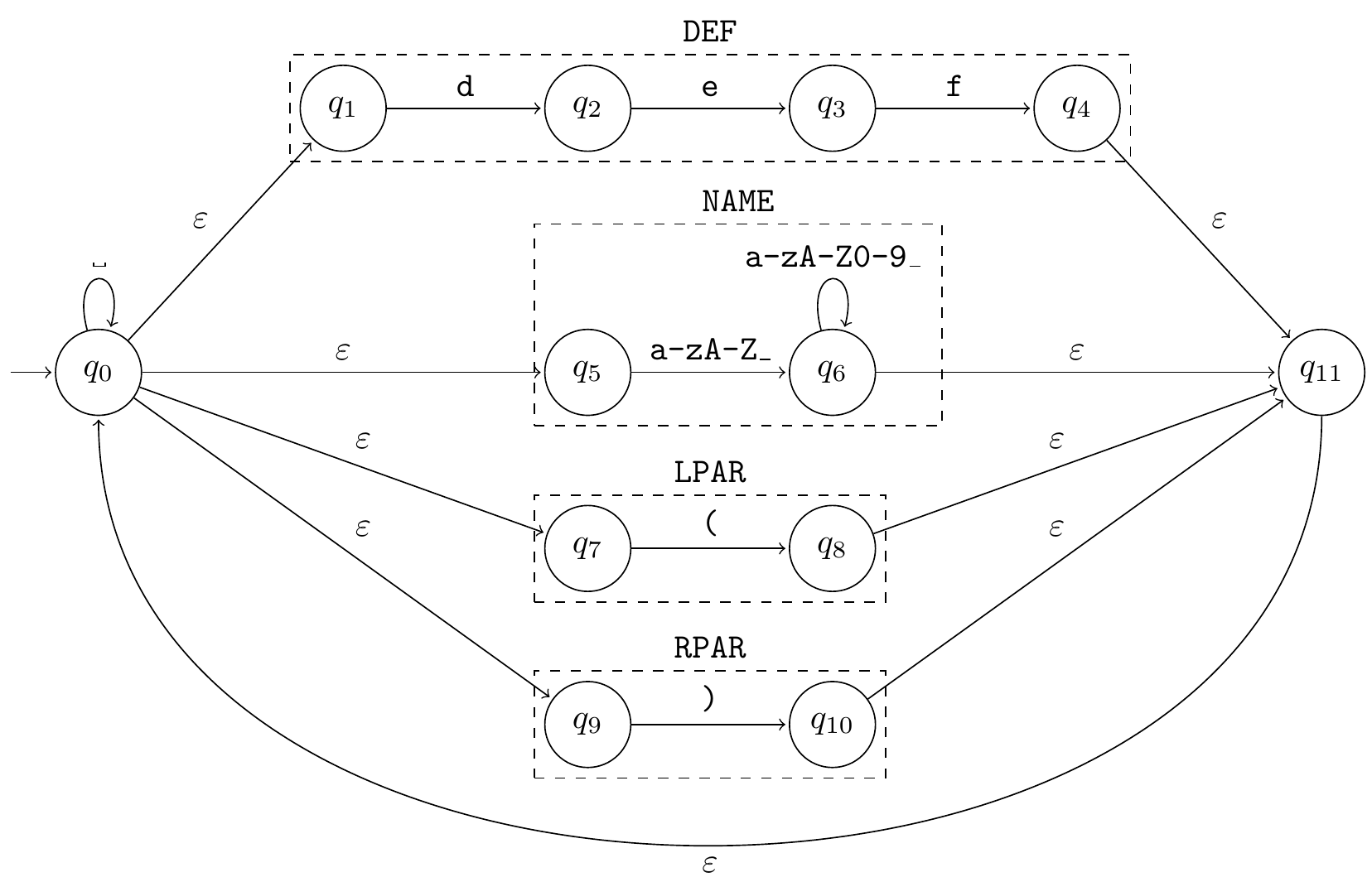
NFA used to identify potential sequences of terminals

Figure 1. Part of a non-deterministic finite automaton used to identify potential sequences of terminals for the Python grammar (the full NFA has 410 states and 2,398 transitions).

Since LLMs manipulate tokens and not characters, we need to convert this character-based NFA into the equivalent token-based NFA. This is done by simply seeing each token as a sequence of characters and applying the corresponding transitions (Willard & Louf, 2023; Beurer-Kellner et al., 2024). For example, if () is a token, the token-based NFA will include () transitions from \(q_0, q_4, q_6, q_8, q_{10}\) and \(q_{11}\) to \(q_{10}\).

While following the character transitions, we keep track of the DFAs traversed to annotate the transitions of the token-based NFA with the corresponding sequences of new terminals. For example, the () transitions would be annotated with [LPAR, RPAR]. Otherwise said, we create nfa_transition, an annotated transition function of the token-based NFA from \(S \times V\) to \((S \times \Sigma^*)^*\) where \(S\) is the set of states of the NFA, \(V\) is the set of tokens and \(\Sigma\) is the set of terminals:

...
nfa_transition[q4][1270] = [(q4, ("DEF",)), (q6, ("NAME",))] # 1270 is the token id for `def`
... 
nfa_transition[q4][470] = [(q10, ("LPAR", "RPAR"))] # 470 is the token id for `()`
...
# For the Python grammar, `nfa_transitions` is defined with 2,837,801 rows.

Checking that the generated sequences of terminals comply with the grammar

At each step of the decoding process, nfa_transitions shows which tokens can eventually lead to a sequence of terminals. Of course, not all sequences of terminals are syntatically valid. We then need to use an incremental parser to only keep sequences of terminals that are compatible with the CFG. In the context of this blog post, we can see such an incremental parser as an object incremental_parser with an internal state incremental_parser.state and two methods:

The incremental parser is used to check whether the terminals that would be added with a certain new token would be acceptable. Instead of assessing this compliance token by token, we can group together tokens that lead to the same additional terminals, check only once this sequence of terminals and mark all these tokens as acceptable if the result is positive. Following (Ugare et al., 2024) and (Beurer-Kellner et al., 2024)1, we can build a mask_store function that maps \((S \times \Sigma^*)\) to \(\{0, 1 \}^{\mid V \mid}\):

...
mask_store[q4][("NAME",)] = [0, ... 1, ..., 1, ..., 0]
#                            ↑      ↑       ↑       ↑
#                            0    1,270   18,641  |V|-1
... 
mask_store[q4][("LPAR", "RPAR")] = [0, ... 1, ..., 0]
#                                   ↑      ↑       ↑
#                                   0     470    |V|-1
...
# For the Python grammar, `mask_store` is defined with 112,283 rows.

The overall constrained decoding algorithm can then be expressed in pseudo Python code as follows.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

def generate(llm, prompt, grammar):

    token_ids = tokenize(prompt)
    new_token_id = None

    # Initialize the states of the lexer and the incremental parser
    lexer_states = [(0, [])] # list of (nfa_state, terminals) tuples
    incremental_parser = IncrementalParser(grammar)

    # Generate one token for each iteration of the while loop
    while new_token_id != eos_token_id:
        
        # Initialize an empty mask
        mask = [0]*len(tokenizer_vocabulary)
        
        # Filter the potential next tokens with the incremental parser
        for nfa_state, terminals in lexer_states:
            for new_terminals in mask_store[nfa_state]:
                if incremental_parser.accepts(terminals + new_terminals):
                    mask = element_wise_binary_or(mask, mask[nfa_state][new_terminals])
        
        # Sample a new token with the LLM and the mask
        # Cf. algorithm 2 of arxiv.org/abs/2307.09702
        new_token_id = llm.sample(token_ids, mask)
        token_ids.append(new_token_id)
        
        # Update the states of the lexer and the incremental parser
        new_states = [
            (new_nfa_state, terminals + new_terminals)
            for new_nfa_state, new_terminals in nfa_transition[nfa_state][token_id]
        ]
        length_common_prefix = get_length_common_prefix(
            [terminals for new_nfa_state, terminals in new_states[new_token_id]]
        )
        incremental_parser.consumes(length_common_prefix)
        lexer_states = [
            (new_nfa_state, terminals[len(length_common_prefix):])
            for new_nfa_state, terminals in new_states[new_token_id]
        ]

    return token_ids

Patterns of Interest to Accelerate Decoding

The reason why constrained decoding is much slower for CFG constraints than for regex constraints is that, at each decoding step, the incremental parser may be called once for each mask of the current NFA states, as shown on lines 17-19 above. In the following, we will see how to significantly reduce the number of calls to the incremental parser.

Consider state \(q_4\) from Figure 1. The mask store contains 1,036 sequences of terminals for this state, which corresponds to the DEF terminal. However, DEF appears only once in the EBNF formalization of the Python grammar – funcdef: "def" name "(" [parameters] ")" ["->" test] ":" suite – and name is defined as name: NAME | "match" | "case". Consequently, only the NAME, "match" and "case" terminals can follow DEF. As a result, DEFfollowed by NAME (or "match" or "case") is always accepted whenever DEF is accepted while DEF followed by ASYNC, CLASS or any other terminal is never accepted, whatever the current parser state is. This means that we can streamline the mask store to avoid superfluous calls to the incremental parser.

...
mask_store[q4][()] = m1
mask_store[q4][("NAME",)] = m2
mask_store[q4][("MATCH",)] = m3
mask_store[q4][("CASE",)] = m4
mask_store[q4][("ASYNC",)] = m5
mask_store[q4][("CLASS",)] = m6
...

… should be simplified as:

...
mask_store[q4][()] = element_wise_binary_or(m1, m2, m3, m4)
...

Let us now consider another interesting pattern of the Python grammar. The MINUS and PLUS terminals only appear in two rules:

!_unary_op: "+"|"-"|"~"
!_add_op: "+"|"-"

Given that MINUS and PLUS are interchangeable in these rules, replacing one with the other does not affect the syntatic correctness of a string. This is another opportunity to streamline the mask store by merging the entries with PLUS and those with MINUS. For example:

...
mask_store[q6][("MINUS",)] = m1
mask_store[q6][("MINUS", "MINUS")] = m2
mask_store[q6][("PLUS",)] = m3
mask_store[q6][("PLUS", "PLUS")] = m4
...

… should be simplified as:

...
mask_store[q6][("MINUS",)] = element_wise_binary_or(m1, m3)
mask_store[q6][("MINUS", "MINUS")] = element_wise_binary_or(m2, m4)
...

We could systematically identify similar patterns if we had access to the following functions:

\[\begin{alignat}{10} \texttt{is_always_legal} \colon\quad &\Sigma\times \Sigma^* \quad&\to&\quad \{\texttt{True}, \texttt{False}\}\\ &(X, S) &\mapsto&\quad (\forall P \in \Sigma^*, PX \in L_p \implies PXS \in L_p)\\ &&&\\ \texttt{is_never_legal} \colon\quad &\Sigma\times \Sigma^* \quad&\to&\quad \{\texttt{True}, \texttt{False}\}\\ &(X, S) &\mapsto&\quad (\forall P \in \Sigma^*, PXS \notin L_p)\\ &&&\\ \texttt{are_jointly_legal} \colon\quad & \Sigma\times \Sigma^*\times \Sigma^* \quad&\to&\quad \{\texttt{True}, \texttt{False}\}\\ &(X, S_1, S_2) &\mapsto&\quad (\forall P \in \Sigma^*, PXS_1 \in L_p \iff PXS_2 \in L_p)\\ \end{alignat}\]

… where \(L\), \(L_p\) and \(\Sigma\) denote the context-free language corresponding to the grammar, the set of prefixes of \(L\) and the set of terminals of \(L\).

The mask store can be streamlined on the basis of these three functions:

We now examine whether it is actually possible to compute \(\texttt{is_always_legal}\), \(\texttt{is_never_legal}\) and \(\texttt{are_jointly_legal}\).

Always Illegal Continuations

The definition of \(\texttt{is_never_legal}\) entails that:

\[\forall X\in \Sigma, S\in \Sigma^*, \texttt{is_never_legal}(X, S) = (L \cap \Sigma^*XS\Sigma^* = \emptyset)\]

Given that \(\Sigma^*XS\Sigma^*\) is a regular language over \(\Sigma\), computing \(\texttt{is_never_legal}\) is equivalent to determining the intersection of a context-free language and a regular language and testing whether this new context-free language is empty. As there are standard algorithms for these two operations, this suggests a straightforward way to obtain \(\texttt{is_never_legal}\):

1
2
3
4
5
6
7
8
9
10
11
12
13
14

def is_never_legal(current_terminal, new_terminals, grammar):
    """
    Return True if `new_terminals` can never follow `current_terminal` given the grammar
    """

    # We create a regular expression defined over the set of terminals, that recognizes
    # any sequence of terminals including `current_terminal` immediately followed by
    # `new_terminals`.
    regex = f".*{current_terminal}{''.join(new_terminals)}.*"

    # The intersection of a context-free grammar and a regular language is a
    # context-free grammar which can be efficiently computed with the Bar-Hillel
    # construction. We can then test its emptiness with a standard CFG algorithm.
    return is_empty(intersection(grammar, regex))

Always Legal Continuations

In contrast, \(\texttt{is_always_legal}\) is not computable as proven in the technical appendix of this blog post. A general algorithm is then out of reach but I outline below \(\texttt{Unlimited credit exploration}\), a method to obtain some values of this function. For the sake of brevity, I restrict myself to a very simple example and focus on conveying the main intuitions, without formalizing the method or proving its correctness. I invite you to read the technical appendix if you are interested in such details.

Let us take the example of the context free grammar corresponding to the \(S::=aSb\mid\epsilon\) rule. The associated context free language is obviously \(\{a^nb^n \mid n\in \mathbb{N}\}\). If we want to determine some values of \(\texttt{is_always_legal}\), it is useful to understand which symbols can follow another symbol. We can describe these relationships with a directed graph, as illustrated in Figure 2.

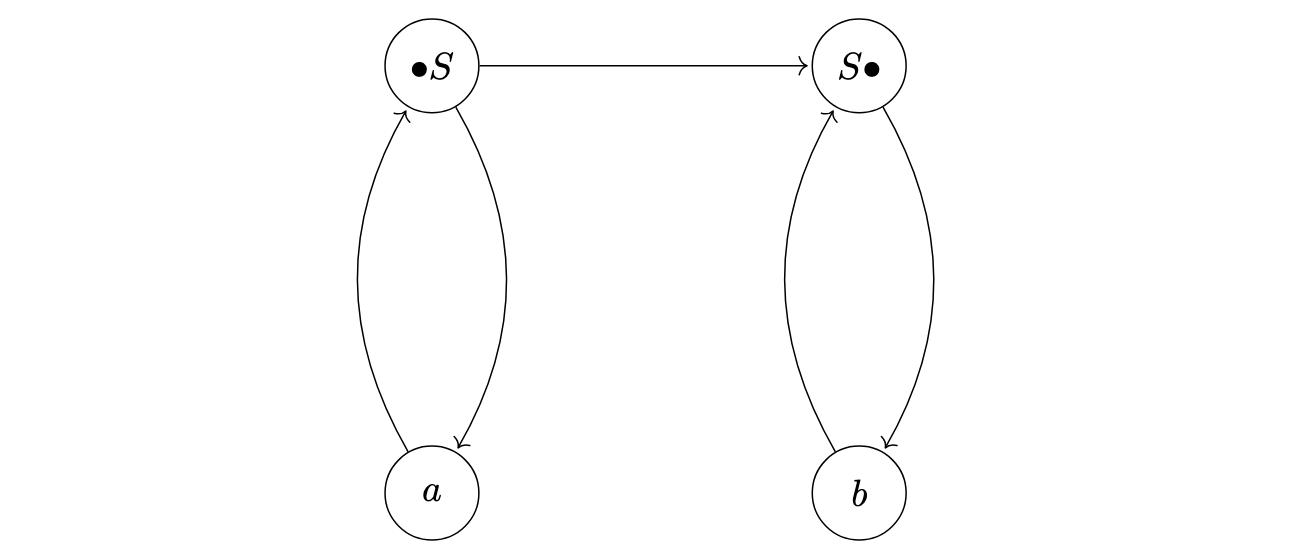
Directed graph showing the direct successor relationship for a grammar

Figure 2. A directed graph showing the direct successor relationship for the grammar corresponding to the \(S::=aSb\mid\epsilon\) rule. \(•S\) and \(S•\) respectively represent the start and the end of nonterminal S.

However, such a directed graph is generally not rich enough to draw conclusions about the values of \(\texttt{is_always_legal}\). To go further, we extend this representation to not only track the successor relationships among symbols but also the rules from which these relationships arise. More precisely, we use the pushdown automaton shown in Figure 3, with \(\bullet S\) and \(Z_0\) as the initial state and stack symbol and \(\texttt{\$END}\) as the only accepting state. In this pushdown automaton, the states represent terminal or nonterminal symbols that are being generated while the stack symbols represent specific locations in the rules of G and serve as “return addresses” to follow once a symbol has been generated.

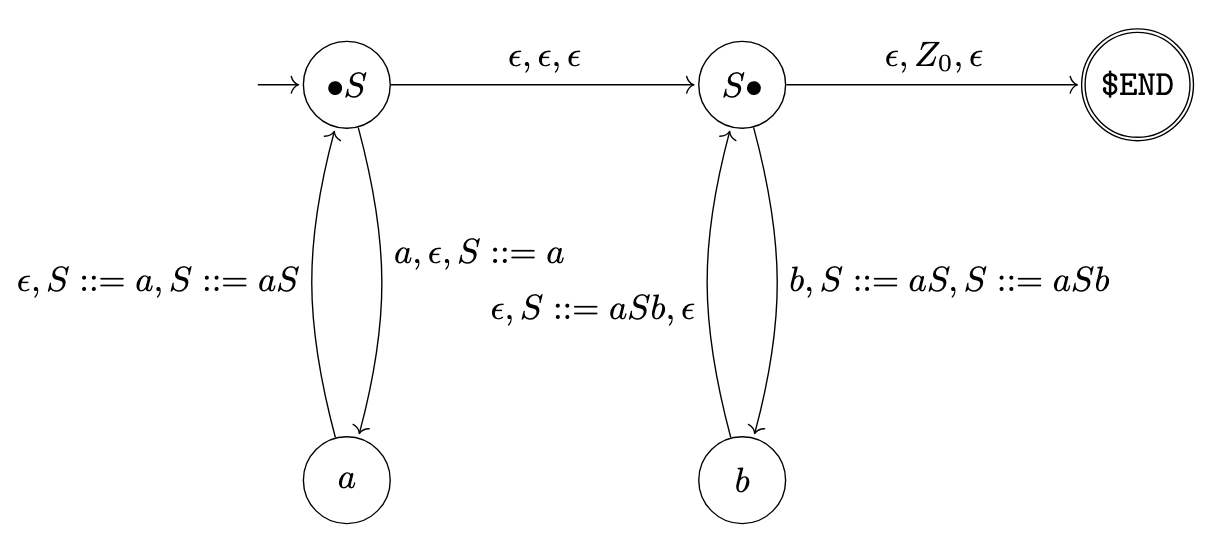
Pushdown automaton for a grammar

Figure 3. A pushdown automaton for the grammar corresponding to the \(S::=aSb\mid\epsilon\) rule. The labels of the edges should be interpreted as a triplet combining the character to read, the stack symbol to pop and the stack symbol to push.

This pushdown automaton has interesting properties for our purpose:

Path of an accepted word

Figure 4. (Left) The pushdown automaton in Figure 3 accepts the word \(aabb\) through the path displayed in the table. (Right) This path corresponds to a left-to-right depth-first traversal of the syntax tree of \(aabb\).

If we want to determine the value of \(\texttt{is_always_legal}(X, Y)\) with \(X, Y \in \Sigma\), the first step is to start at the \(X\) state with an empty stack and list all the paths reading \(Y\) through the pushdown automaton. For this, we follow the step relation of the pushdown automaton, except that, if the stack is empty and we need to pop a stack symbol, we still proceed with the transition and take note of the missing stack symbol. It is as if we had an unlimited line of credit to borrow stack symbols when the stack is empty. We also define a maximum stack size during the search so that it is guaranteed to terminate.

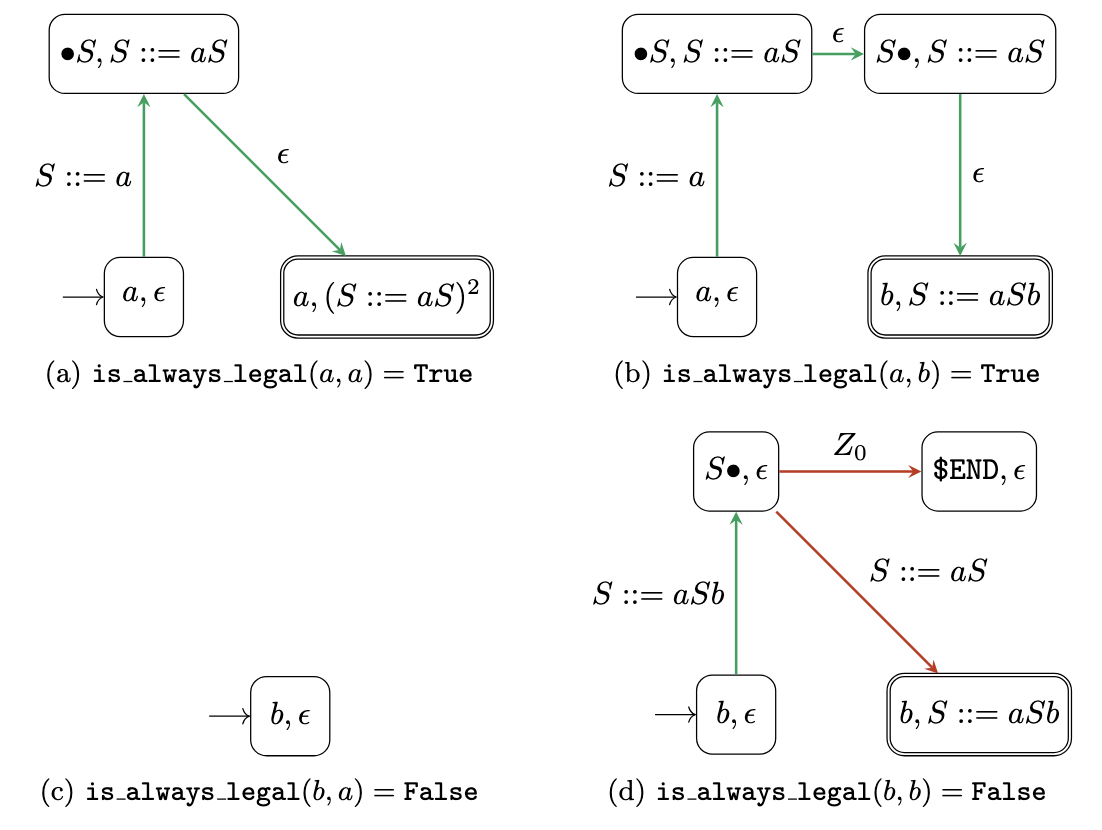
The second step is to represent all these paths as a non-deterministic finite automaton (NFA) as shown in Figure 5: the nodes correspond to the combination of a state of the pushdown automaton and the associated stack, the start node is \((X, \epsilon)\), the accepting nodes are \(Y\) with any stack and the transitions are either \(\epsilon\) or a missing stack symbol identified along a path.

The third and last step is to identify the \(\epsilon\)-coaccessible nodes of the NFA, i.e. the nodes that satisfy one of the following properties:

A sufficient condition for \(\texttt{is_always_legal}(X, Y) = \texttt{True}\) is then that \((X, \epsilon)\) is \(\epsilon\)-coaccessible. Figure 5 shows the NFAs obtained for \(X = a, Y = a\), \(X = a, Y = b\), \(X = b, Y = a\), \(X = b, Y = b\). Since \(S::=a\) is the only stack symbol that can be popped from \(a\) in the pushdown automaton, we can conclude that \(\texttt{is_always_legal}(a, a) = \texttt{is_always_legal}(a, b) = \texttt{True}\). This is not the case for \(X = b, Y = a\) and \(X = b, Y = b\) and it is indeed easy to show that \(\texttt{is_always_legal}(b, a) = \texttt{is_always_legal}(b, b) = \texttt{False}\).

The intuition behind this approach is that the NFA captures the stack symbols needed to move from \(X\) to \(Y\). Along such a trajectory, the conditions defined above ensure that we can always move one step closer to \(Y\), either because we can move forward with an \(\epsilon\) transition or because there is a relevant transition for each possible stack symbol on top of the stack.

Non-deterministic finite automata

Figure 5. The non-deterministic finite automata corresponding to \(\texttt{is_always_legal}(a, a)\), \(\texttt{is_always_legal}(a, b)\), \(\texttt{is_always_legal}(b, a)\) and \(\texttt{is_always_legal}(b, b)\).

Jointly Legal Continuations

Like \(\texttt{is_always_legal}\), \(\texttt{are_jointly_legal}\) is not computable because the values of \(\texttt{is_always_legal}\) can directly be derived from those of \(\texttt{are_jointly_legal}\). Indeed, for all \(X\in\Sigma, Y\in\Sigma^*\):

\[\texttt{is_always_legal}(X, Y) = \texttt{are_jointly_legal}(X, Y, \epsilon)\]

There are however simple ways to get some values of \(\texttt{are_jointly_legal}\). First we can use known values of \(\texttt{is_always_legal}\), e.g. \(\texttt{is_always_legal}(Y_1, Y_2) = \texttt{True}\), to conclude that:

\[\texttt{are_jointly_legal}(X, X_1...X_nY_1Y_2, X_1...X_nY_1) = \texttt{True} \text{ for all } X, X_1,..., X_n \in \Sigma\]

For example, using the method described in the previous section, we can show that \(\texttt{is_always_legal}(\texttt{MINUS}, (\texttt{MINUS},)) = \texttt{True}\) for the Python grammar. As a consequence:

\[\texttt{are_jointly_legal}(\texttt{NAME}, (\texttt{MINUS},), (\texttt{MINUS}, \texttt{MINUS})) = \texttt{True}\] \[\texttt{are_jointly_legal}(\texttt{NAME}, (\texttt{MINUS},), (\texttt{MINUS}, \texttt{MINUS}, \texttt{MINUS})) = \texttt{True}\] \[...\]

Furthermore, we can take advantage of the fact that some terminals are interchangeable in the rules of the grammar. For example, the only rules of the Python grammar with the \(\texttt{PLUS}\) and \(\texttt{MINUS}\) terminals are:

!_unary_op: "+"|"-"|"~"
!_add_op: "+"|"-"

This means that it is always possible to replace one \(\texttt{PLUS}\) terminal with a \(\texttt{MINUS}\) terminal (and vice versa), without affecting the syntactical correctness of a sequence of terminals. If we can determine that terminals \(Y_1\) and \(Y_2\) are interchangeable, we can conclude that:

\[\texttt{are_jointly_legal}(X, X_1...X_n, \phi(X_1)...\phi(X_n)) = \texttt{True} \text{ for all } X, X_1,..., X_n \in \Sigma\]

… where \(\phi(Y_1) = Y_2\) and \(\phi(X) = X\) if \(X\neq Y_1\).

With the Python grammar, there are seven sets of mutually interchangeable terminals, containing 35 terminals in total:

1: "/=", "%=", "^=", "**=", "*=", ">>=", "|=", "-=", "+=", "//=", "<<=", "@=", "&="
2: FALSE, NONE, TRUE
3: PLUS, MINUS
4: "<<", ">>"
5: "//", PERCENT
6: "!=", LESSTHAN, ">=", "==", "<=", MORETHAN, "<>"
7: HEX_NUMBER, FLOAT_NUMBER, BIN_NUMBER, OCT_NUMBER, DEC_NUMBER, IMAG_NUMBER

Experimental Results

The accompanying Python notebook evaluates the effectiveness of mask store streamlining. Since some of the operations are time-computing, in particular the computation of \(\texttt{is_never_legal}\) (because it requires taking into account the whole grammar whereas using \(\texttt{Unlimited credit exploration}\) only leverages local relationships in the pushdown automaton), I proceeded in the following way:

Figure 6 shows that these steps combined result in a ten-fold reduction of the size of the mask store.

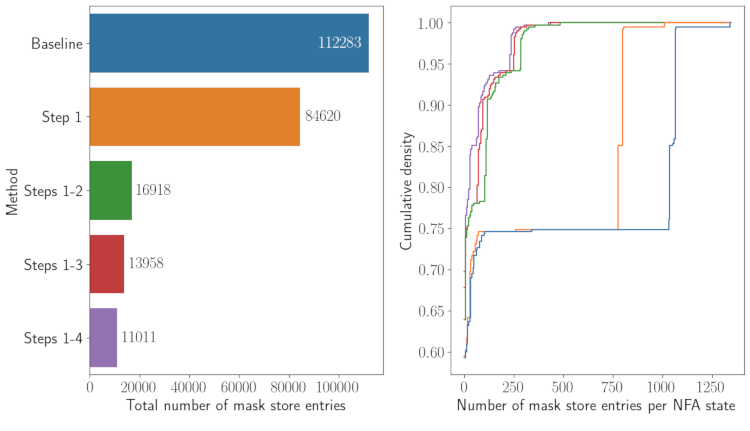
Number of mask store entries according to the streamlining method

Figure 6. (Left) Number of mask store entries according to the streamlining method. (Right) Cumulative distribution of the number of mask store entries per NFA state, according to the streamlining method.

Furthermore, I performed three experiments to confirm that streamlining the mask store yields valid results:

These three experiments were successful, which suggests, as expected, that the masks computed are adequate (i.e. neither excessively restrictive nor excessively permissive) and that streamlining the mask store does not alter the masks computed at decoding time.

Conclusion and Potential Future Work

This post introduces a novel method for streamlining mask stores in CFG-constrained decoding techniques that leverage an automaton-based lexer and an incremental parser. This method significantly reduces the inference overhead at the cost of modest additional computations performed once for a given grammar and a given tokenizer.

Potential areas for improvement of this method are as follows:

Thanks to the authors of the papers mentioned below and to the contributors of the various packages used in this project (inter alia, \(\texttt{outlines}\), \(\texttt{interegular}\), \(\texttt{lark}\) and \(\texttt{pyformlang}\)). I am also particularly grateful to Martin Berglund who right away suggested a potential undecidability problem when I let him know of my investigations.

If you want to cite this blog post, you are welcome to use the following BibTeX entry:

@misc{Tran-Thien_2025,
title={Accelerating LLM Code Generation Through Mask Store Streamlining},
url={https://vivien000.github.io/blog/journal/grammar-llm-decoding.html},
journal={Unsupervised Thoughts (blog)},
author={Tran-Thien, Vivien},
year={2025}
}

References

  1. Willard, B. T., & Louf, R. (2023). Efficient Guided Generation for Large Language Models.
  2. Gerganov, G., & et. al. (2024). llama.cpp: Inference of Meta’s LLaMA model (and others) in pure C/C++. https://github.com/ggerganov/llama.cpp
  3. Lundberg, S., & Ribeiro, M. T. C. et al. (2023). Guidanceai/guidance: A guidance language for controlling large language models. https://github.com/guidance-ai/guidance
  4. Geng, S., Josifoski, M., Peyrard, M., & West, R. (2024). Grammar-Constrained Decoding for Structured NLP Tasks without Finetuning. https://arxiv.org/abs/2305.13971
  5. Beurer-Kellner, L., Fischer, M., & Vechev, M. (2024). Guiding LLMs The Right Way: Fast, Non-Invasive Constrained Generation. https://arxiv.org/abs/2403.06988
  6. Ugare, S., Suresh, T., Kang, H., Misailovic, S., & Singh, G. (2024). SynCode: LLM Generation with Grammar Augmentation. https://arxiv.org/abs/2403.01632
  7. Dong, Y., Ruan, C. F., Cai, Y., Lai, R., Xu, Z., Zhao, Y., & Chen, T. (2024). XGrammar: Flexible and Efficient Structured Generation Engine for Large Language Models. https://arxiv.org/abs/2411.15100

  1. The Domino algorithm (Beurer-Kellner et al., 2024) introduces subterminal trees which are analogous to mask stores organized as prefix trees. Using a prefix tree helps avoid unnecessary calls to the incremental parser but this distinction is not essential in the context of this blog post. ↩

Written on January 3rd , 2025 by Vivien
Feel free to share!
comments powered by Disqus