Unsupervised Thoughts A blog on machine learning
Fast, High-Fidelity LLM Decoding with Regex Constraints

Constraining the text generated by an LLM is essential for developing robust LLM applications. For example, a developer may require LLM responses to adhere to a specific JSON or YAML schema so that they are comprehensive and reliably parseable.
Powerful tools and methods (Beurer-Kellner et al., 2022; Lundberg & Ribeiro, 2023; Willard & Louf, 2023; Zheng et al., 2023) have been published in the past year to address this need. Notably, the open source library \(\texttt{Outlines}\) implements an efficient method (Willard & Louf, 2023) that ensures compliance with an arbitrary regex.
In this blog post, I propose two novel, fast, high-fidelity alternatives to this method. Specifically, I will:
- Present the principle of \(\texttt{Outlines}\)1 and discuss how allowing improper token sequences (i.e. token sequences that do not correspond to the tokenization of a string) can skew the probability distribution of the LLM and hinder the decoding speed;
- Introduce \(\texttt{DirectMerge}\), a method that maintains guaranteed compliance while only generating proper token sequences. \(\texttt{DirectMerge}\) is valid for all tokenizers based on a merge table and in particular for the very popular Byte Pair Encoding tokenizers (Sennrich et al., 2016);
- Propose \(\texttt{CartesianMerge}\), a variant of \(\texttt{DirectMerge}\) that scales better with the complexity of the regex;
- Discuss the execution time of \(\texttt{CartesianMerge}\) and show how this execution time can be significantly reduced in the case of a JSON or YAML schema constraint.
This blog post comes with a technical appendix formalizing and proving the algorithms. Additionally, a Python notebook with implementations of \(\texttt{DirectMerge}\) and \(\texttt{CartesianMerge}\), along with additional empirical results, is available.
- Deterministic Finite Automata and Constrained Decoding
- Three Challenges due to Improper Token Sequences
- Ensuring Both Compliance and Proper Tokenization
- Scaling with the Complexity of the Regex
- Is it Fast Enough?
- Conclusion
- References
Deterministic Finite Automata and Constrained Decoding
I now briefly explain the principle of \(\texttt{Outlines}\). Please read the original paper (Willard & Louf, 2023) or this blog post for a more comprehensive overview.
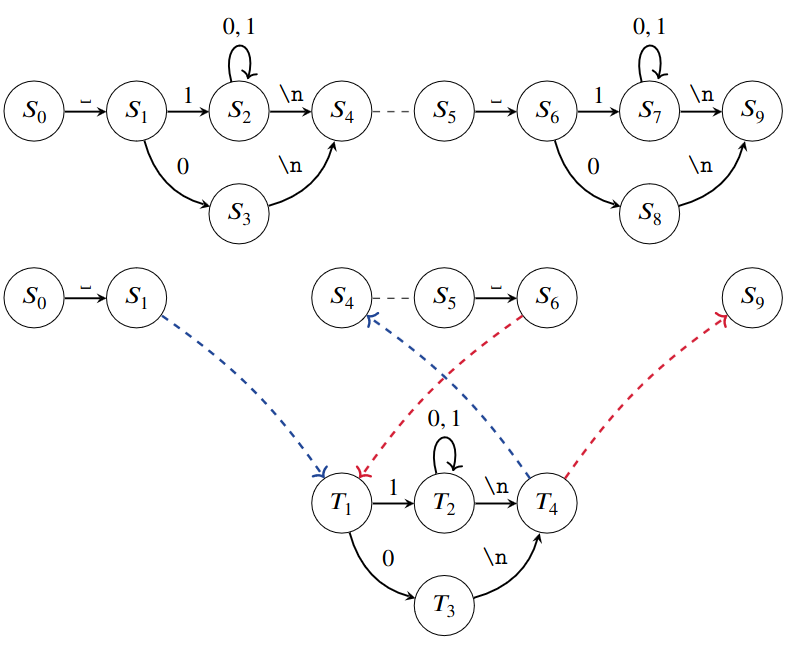
As a preprocessing step, \(\texttt{Outlines}\) converts a character-level deterministic finite automaton (DFA) testing whether a string matches a regex (cf. Figure 1a) into a token-level DFA testing whether a token sequence is decoded in a string matching the regex (cf. Figure 1b):
- the states, including the start state and the accept states, remain the same;
- the alphabet of the token-level DFA is the tokenizer’s vocabulary;
- the transition function of the token-level DFA is the extended transition function of the character-level DFA restricted to the tokenizer’s vocabulary. For example with the example of Figure 1b, there is an \(\texttt{abb}\) transition from \(\texttt{0}\) to \(\texttt{1}\) because if we start from \(\texttt{0}\) on the character-level DFA and successively see \(\texttt{a}\), \(\texttt{b}\) and \(\texttt{b}\), we’ll end up in state \(\texttt{1}\).
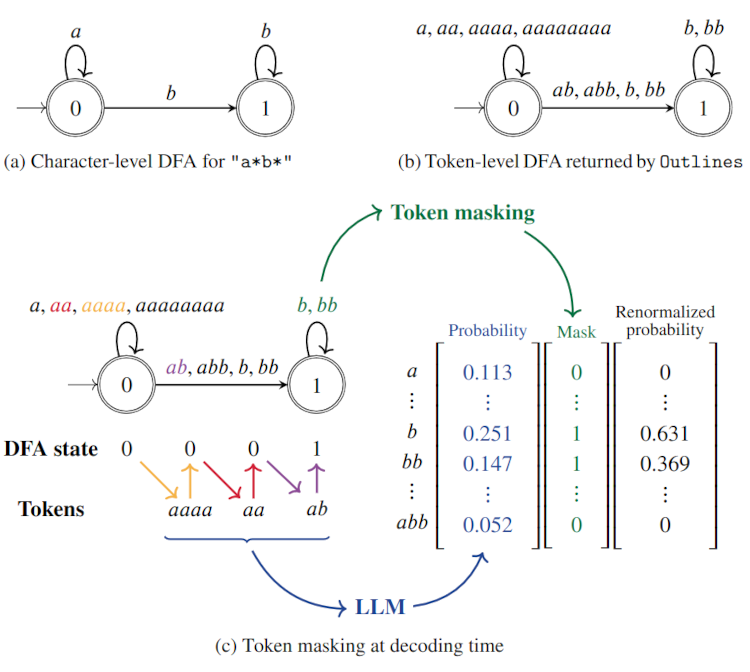
At decoding time, the DFA is used to determine, for each new token, which potential tokens are allowed. For this and starting from the initial state of the DFA, we determine the allowed tokens with the outgoing transitions from the current state, apply the corresponding mask to the next token probabilities and renormalize these probabilities. We can then sample a new token and update the state of the DFA.
For example, let’s imagine that the tokens \(\texttt{aaaa}\), \(\texttt{aa}\) and \(\texttt{ab}\) have already been generated. Starting from state \(\texttt{0}\), we remained in state \(\texttt{0}\) with \(\texttt{aaaa}\) and \(\texttt{aa}\) but transitioned to state \(\texttt{1}\) with \(\texttt{ab}\). The tokens now allowed are simply those with an outgoing transition from state \(\texttt{1}\), i.e. \(\texttt{b}\) and \(\texttt{bb}\). We then consider the next token probabilities of these two tokens and we renormalize them so that they sum to 1.
Three Challenges due to Improper Token Sequences
The token sequences potentially generated with \(\texttt{Outlines}\) are exactly those that are decoded into a string matching the regex. This includes token sequences that do not result from the tokenization of a string. We call them improper token sequences below.
Consider the regex: \(\texttt{"boolean: ((true)}\mid\texttt{(false))"}\). While there are only two strings matching this regex, the corresponding DFA returned by \(\texttt{Outlines}\) has 16 states and 48 transitions (Figure 2). For example, the first token is chosen among \(\texttt{boolean}\), \(\texttt{bool}\), \(\texttt{bo}\) and \(\texttt{b}\).
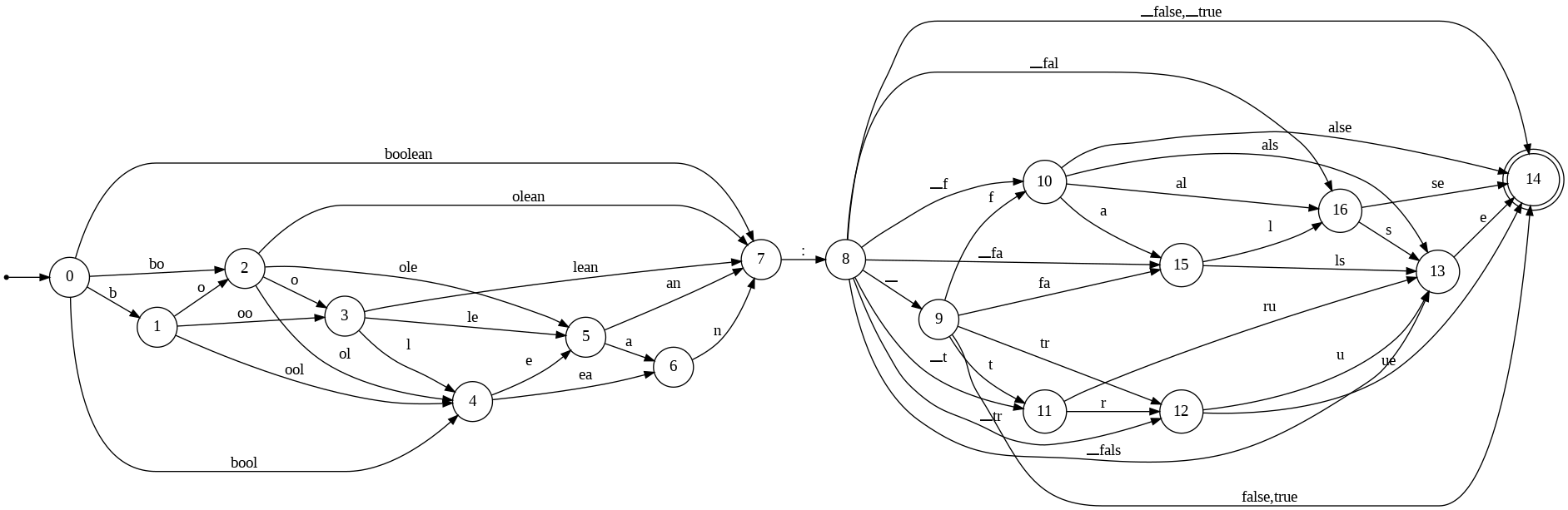
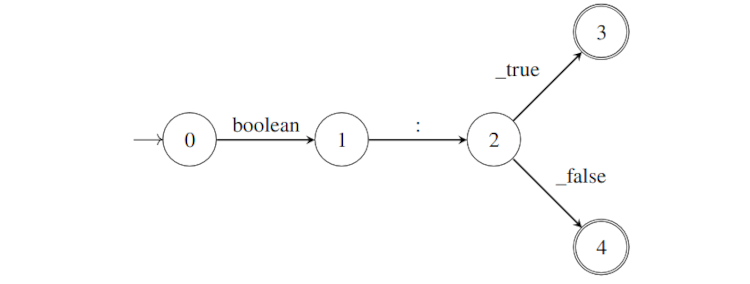
In contrast, as we will see in the following sections, the DFA built by \(\texttt{DirectMerge}\) and \(\texttt{CartesianMerge}\) only accepts the token sequences resulting from the tokenization of compliant strings and it has only 2 states and 4 transitions (Figure 3).
Challenge #1: Skewed Probability Distribution
The permissiveness of \(\texttt{Outlines}\) with improper token sequences may significantly distort the probability distribution of the LLM, beyond what is strictly necessary to enforce the regex constraint.
To illustrate this, let’s imagine that we generate a continuation of the prompt Question: What is the first name of the US president who was a member of the Sigma Alpha Epsilon fraternity?\nAnswer: with the regex constraint \(\texttt{"( William)}\mid \texttt{( Theodore)"}\) (the true answer is William like William McKinley, Theodore Roosevelt’s predecessor).
When the text generation is unconstrained, we can compute the probability along all token sequences leading to one of the two possible answers. If we do so with \(\texttt{Mistral-7B}\) and a temperature equal to 1, we get \(\frac{P(\texttt{" William"})}{P(\texttt{" William"})+P(\texttt{" Theodore"})} = 0.85879\) and notice that almost all the probability mass for these two answers comes from proper token sequences (99.8586% for \(\texttt{" Theodore"}\) and 99.9997% for \(\texttt{" William"}\)).
If we constrain the text generation with \(\texttt{Outlines}\) and multinomial sampling as a decoding strategy, any prefix of \(\texttt{" William"}\) and \(\texttt{" Theodore"}\) will be accepted as the first token and determine the answer (if this first token is not the blank space). For example, the token \(\texttt{" The"}\) can be selected as the first token and in this case, the answer will necessarily be \(\texttt{" Theodore"}\). As a result, the probability to generate \(\texttt{" Theodore"}\) will be the sum of generating \(\texttt{" T"}\), \(\texttt{" Th"}\), \(\texttt{" The"}\), etc. as the first token, even though these first tokens, except \(\texttt{" Theod"}\) almost never lead to \(\texttt{" Theodore"}\) and \(\texttt{" Theodore"}\) will be significantly boosted by the sole virtue of having a very common token, \(\texttt{" The"}\), as a prefix. Indeed, \(\frac{P(\texttt{" William"})}{P(\texttt{" William"})+P(\texttt{" Theodore"})} = 0.52852\) in this case.
With \(\texttt{DirectMerge}\) and \(\texttt{CartesianMerge}\), only the tokens corresponding to the tokenization of the possible answers are taken into account (e.g. \(\texttt{" The"}\) is ignored). The conditional probability, \(\frac{P(\texttt{" William"})}{P(\texttt{" William"})+P(\texttt{" Theodore"})} = 0.85872\), is very close the one in the unconstrained case, which makes sense given that the LLM spontaneously generates proper token sequences a large majority of the time.
Challenge #2: Self-Intoxication
Another concern is that the tokens generated are fed back to the LLM to select the following ones. During its pretraining and depending whether subword regularization techniques like BPE-Dropout (Provilkov et al., 2020) have been used, an LLM was never or rarely exposed to improper token sequences so this LLM may not properly interpret the newly added tokens and this can impact the quality of its output.
Challenge #3: Missed Speedup Opportunities
As suggested by two recent blog posts, \(\texttt{Outlines}\) offers opportunities to accelerate decoding.
Let’s go back to the DFA provided by \(\texttt{DirectMerge}\) and \(\texttt{CartesianMerge}\) on Figure 3. There is only one outgoing transition from states \(\texttt{0}\) and \(\texttt{1}\). This means that we don’t even need to compute the next token probability when we reach these states since there is only one possible token. We can then generate the whole text in just one LLM call. Meanwhile, the DFA built with \(\texttt{Outlines}\) for the same regex on Figure 2 has 16 states but only 3 states with one outgoing transition (states 6, 7 and 13). There are then much fewer opportunities to skip computationally expensive LLM calls. Moreover, there are many potential paths that are much longer than three transitions. This can also slow down the decoding.
Ensuring Both Compliance and Proper Tokenization
We can now focus on \(\texttt{DirectMerge}\). Even though its aims are slightly different, \(\texttt{DirectMerge}\) shares the same overall approach as \(\texttt{Outlines}\): it derives a token-level DFA from a character-level DFA recognizing the regex and this token-level DFA is used to identify allowed tokens at decoding time.
\(\texttt{DirectMerge}\) applies to tokenizers based on a merge table, like Byte Pair Encoding tokenizers (Sennrich et al., 2016). Encoding a string with such tokenizers consists of converting the string into a sequence of single-letter tokens and then performing an ordered list of merge operations. Each of these merge operations is defined by two tokens (e.g. \(\texttt{a}\) and \(\texttt{b}\)) and merge all the corresponding pairs of consecutive tokens, starting from the left of the current token sequence.
| Initial string | \(\texttt{aaaabaacac}\) |
| Conversion to a sequence of single-letter tokens | \(\texttt{a a a a b a a c a c}\) |
| Token sequence after \(\texttt{merge}(\texttt{a}, \texttt{b})\) | \(\texttt{a a a }\underline{\texttt{ab}}\texttt{ a a c a c}\) |
| Token sequence after \(\texttt{merge}(\texttt{a}, \texttt{a})\) | \(\underline{\texttt{aa}}\texttt{ a ab }\underline{\texttt{aa}}\texttt{ c a c}\) |
| Final token sequence after \(\texttt{merge}(\texttt{a}, \texttt{c})\) | \(\texttt{aa a ab aa c }\underline{\texttt{ac}}\) |
With \(\texttt{DirectMerge}\), we start with the character-level DFA and we apply a series of simple transformations for each merge operation. Let us consider the case of an \((a, b)\) merge operation with \(a \neq b\). \(\texttt{DirectMerge}\) affects each state \(S\) with one or several incoming \(a\) transitions and one outgoing \(b\) transition and its impact depends on two criteria:
- Has \(S\) non-\(a\) incoming transitions or is \(S\) the start state?
- Has \(S\) non-\(b\) outgoing transitions or is \(S\) an accept state?
More precisely and if the outgoing \(b\) transition from \(S\) leads to \(S_b\), the transformations applied to state \(S\) are the following:
- Replace each incoming \(a\) transition by an \(ab\) transition to \(S_b\)
- If both criteria are false (cf. Figure 4a):
- Remove \(S\)
- If Criterion 1 is false and Criterion 2 is true:
- Remove the outgoing \(b\) transition
- If Criterion 1 is true and Criterion 2 is false:
- Remove all incoming \(a\) transitions
- If both criteria are true (cf. Figure 4c):
- Add a state \(S'\)
- Redirect all incoming \(a\) transitions to \(S'\)
- Copy all non-\(b\) transitions of \(S\) and add them to \(S'\)
- Make \(S'\) an accept state if \(S\) is an accept state
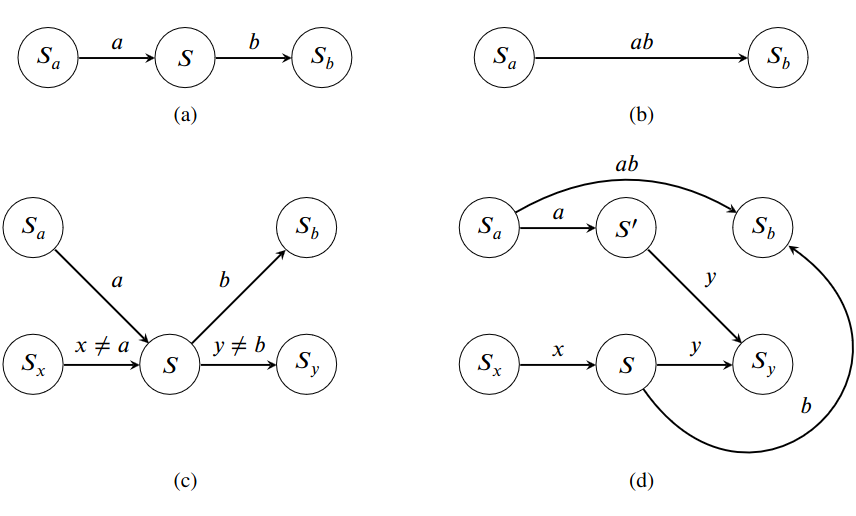
The case of merge operations with two identical tokens is more challenging because not all pairs of matching tokens should be merged. For example, on the fourth row of Table 1 above, the second and third \(a\) are not merged because the merge operation is applied left-to-right and the second \(a\) is already merged with the first \(a\). You can find the description of \(\texttt{DirectMerge}\) in the case \(a = b\) and the correctness proof for both cases in the technical appendix.
Scaling with the Complexity of the Regex
\(\texttt{DirectMerge}\) guarantees both compliance with the regex constraint and proper tokenization. However, \(\texttt{DirectMerge}\) removes or adds states and transitions and in some unfavorable circumstances, the number of states and transitions may become overwhelmingly large.
Fortunately, with \(\texttt{CartesianMerge}\), we can efficiently simulate the DFA created by \(\texttt{DirectMerge}\) without explicitly building it. We can indeed notice that the target language is the intersection of the set of all token sequences decoded into strings matching the regex and the set of all proper token sequences. Both of these sets are regular languages and we already know how to build the corresponding DFAs, with \(\texttt{Outlines}\) for the first one and with \(\texttt{DirectMerge}\) applied to the \(\texttt{".*"}\) regex for the second one. Furthermore, as opposed to the DFA returned by \(\texttt{DirectMerge}\), they will not become uncontrolably large as the regex becomes more complex. \(\texttt{Outlines}\) does not add any state to the character-level DFA and the DFA returned by \(\texttt{DirectMerge}\) with \(\texttt{".*"}\) happens to have interesting properties that make it easy to compute and compress (cf. the technical appendix for more details).
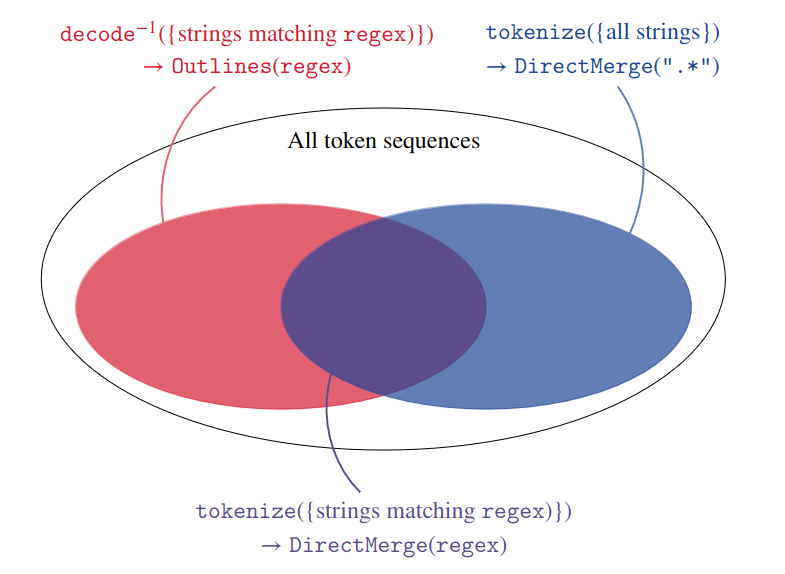
Once we have built these two DFAs, we can keep track of their respective states at decoding time and the allowed tokens are in the intersection of their respective sets of allowed tokens.
However, knowing which tokens are valid transitions in both DFAs is not enough because we also need to check that the tokens generated can eventually lead to a token sequence decoded into a string matching the regex. This was not an issue before because both \(\texttt{Outlines}\) and \(\texttt{DirectMerge}\) generate token-level DFAs whose states are all relevant (i.e. on a path between the start state and an accept state) as long as the initial character-level DFA only has relevant states. The pairs of states that are valid can be computed with a breadth-first exploration starting from the pair of start states and then from the pairs of accept states with reverse transitions.
Is it Fast Enough?
Table 2 reports the execution time of the various steps of \(\texttt{CartesianMerge}\) for a sample of JSON strings from the \(\texttt{glaive-function-calling-v2}\) dataset. The delay of the first step is negligible because this activity only needs to be executed once for a given tokenizer and its outcome will be useful for all future regex. The second and fourth steps also add little overhead while the third step is the performance bottleneck.
| Step | Activity | Mean duration (seconds) | Comment |
|---|---|---|---|
| 1 | Compute the DFA recognizing proper token sequences with \(\texttt{DirectMerge}\) (preprocessing) | 20.9 | Only once for a given tokenizer |
| 2 | Compute the DFA recognizing the token sequences decoded into strings matching the regex with \(\texttt{Outlines}\) (preprocessing) | 0.687 | Only once for a given regex |
| 3 | Identify relevant pairs of states (preprocessing) | 27.3 | Only once for a given regex |
| 4 | Build the token mask (decoding) | 0.00153 | At each decoding step |
The latency of the third step remains limited if the regex constraint is used a large number of times but it may become an issue when a new regex is expected to be provided only at the time of decoding. It would typically be the case if an LLM provider offers a feature similar to OpenAI’s function calling. However, when the real goal is to adhere to a JSON or YAML schema, we can significantly shorten the preprocessing.
Oftentimes in practical situations, there will be parts of the regex surrounded by two delimiters with which they cannot merge. This is particularly interesting for us because we then know that the portion of the DFA representing these parts is unaffected by all other parts of the regex. Let’s call these situations Vegas configurations (because what happens between the delimiters stays between the delimiters).
For example with the Mistral-7B tokenizer, whatever string starting with a blank space and delimited by a colon and a line break is a Vegas configuration and this is of course very useful for YAML schemas.
Vegas configurations can be leveraged in two ways, as illustrated by Figure 6:
- if we realize that the same Vegas configuration appears several times in the regex, we can compute and store the corresponding portion of the DFA only once;
- if the variable parts of the regex we use often correspond to a limited number of Vegas configuration, we can build a library of these Vegas configurations, store the corresponding portions of the DFA and directly use them needed. With JSON or YAML schemas, the library would typically include the Vegas configurations of the common types (strings, numbers, dates…).
Conclusion
In this blog post, I introduced two alternatives to \(\texttt{Outlines}\). \(\texttt{DirectMerge}\) and \(\texttt{CartesianMerge}\) also guarantee compliance with a regex constraint while accelerating decoding and mitigating the risks of distortions2 of the language model distribution.
It is unclear how often such distortions may happen. However it is easy to find examples of them and should they happen in practice, they would probably go unnoticed. Given that uncertainty and the decoding speedup, \(\texttt{CartesianMerge}\) should be a no-regret option for most constrained decoding needs.
Beyond constrained decoding, it would also be interesting to assess whether the fact that models sometimes generate improper token sequences affect their performance. If it were the case, \(\texttt{CartesianMerge}\) may be used to enforce proper tokenization.
Thanks to the authors of the papers mentioned below, in particular to Luca Beurer-Kellner for a helpful discussion, and to the contributors of the various resources used (inter alia, \(\texttt{outlines}\), \(\texttt{interegular}\), \(\texttt{transformers}\) and \(\texttt{glaive-function-calling-v2}\)).
If you want to cite this blog post, you are welcome to use the following BibTeX entry:
@misc{Tran-Thien_2024,
title={Fast, High-Fidelity LLM Decoding with Regex Constraints},
url={https://vivien000.github.io/blog/journal/llm-decoding-with-regex-constraints.html},
journal={Unsupervised Thoughts (blog)},
author={Tran-Thien, Vivien},
year={2024}
}
References
- Beurer-Kellner, L., Fischer, M., & Vechev, M. (2022). Prompting Is Programming: A Query Language For Large Language Models. PLDI ’23.
- Lundberg, S., & Ribeiro, M. T. C. et al. (2023). Guidanceai/guidance: A guidance language for controlling large language models. https://github.com/guidance-ai/guidance
- Willard, B. T., & Louf, R. (2023). Efficient Guided Generation for Large Language Models.
- Zheng, L., Yin, L., Xie, Z., Huang, J., Sun, C., Yu, C. H., Cao, S., Kozyrakis, C., Stoica, I., Gonzalez, J. E., Barrett, C., & Sheng, Y. (2023). Efficiently Programming Large Language Models using SGLang.
- Sennrich, R., Haddow, B., & Birch, A. (2016). Neural Machine Translation of Rare Words with Subword Units. In K. Erk & N. A. Smith (Eds.), Proceedings of the 54th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers) (pp. 1715–1725). Association for Computational Linguistics. https://doi.org/10.18653/v1/P16-1162
- Provilkov, I., Emelianenko, D., & Voita, E. (2020). BPE-Dropout: Simple and Effective Subword Regularization. In D. Jurafsky, J. Chai, N. Schluter, & J. Tetreault (Eds.), Proceedings of the 58th Annual Meeting of the Association for Computational Linguistics (pp. 1882–1892). Association for Computational Linguistics. https://doi.org/10.18653/v1/2020.acl-main.170
-
In this blog post, I abusively use \(\texttt{Outlines}\) to denote the underlying method (Willard & Louf, 2023) rather than the open source library. ↩
-
As illustrated in the second section, distortion here means a discrepancy between the probability distribution with constrained decoding — \(P_\text{constrained}(.)\) — and the probability distribution with unconstrained decoding conditioned on the satisfaction of the constraint — \(P_\text{unconstrained}(.\mid\mathcal{S})\) (where \(S\) is the set of the compliant strings). ↩